Логическая задача про монеты

Логическая задача про монеты понравится всем, кто любит логику и понимает пользу головоломок для саморазвития. Если вы до сих пор не были знакомы с этой задачей, то остается только позавидовать тому удовольствию, которое вы получите от ее решения.

Сразу нужно сказать, что никаких подвохов ни в условии, ни в самом решении нет. Поэтому сосредоточившись, активируйте все свои логические способности и приступайте к поиску единственно верного и чрезвычайно изящного решения.

Условия задачи

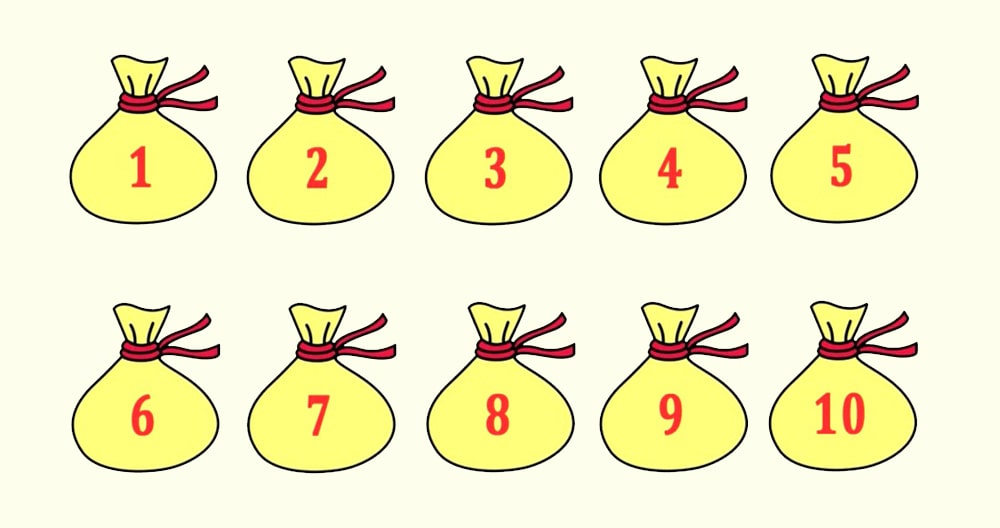
Перед нами 10 пронумерованных мешков, в каждом из которых находится по 10 золотых монет. Каждая монета весит 10 граммов.

В одном из мешков находятся фальшивые монеты. По виду они ничем не отличаются от настоящих, вот только весят они не по 10, а по 11 граммов.

Суть этой логической задачи заключается в том, чтобы при помощи весов найти мешок с фальшивыми монетами. Монеты из мешков можно сколько угодно вынимать и как угодно перекладывать. Казалось бы, дело за малым.

Но вот главное условие, которое делает задачу довольно сложной: взвешивание можно произвести только один раз.

Logicheskaya-zadacha-pro-monety

Напомним, что данная головоломка предполагает абсолютно точное решение, поэтому не тратьте время на поиск какого-то подвоха – его тут просто нет. Решается задача исключительно при помощи логического мышления.

Делитесь в комментариях ходом своих рассуждений, чтобы любой желающий мог либо подтвердить, либо опровергнуть ваше решение.

Что же, удачи вам, и пожалуйста, не ищите готовые ответы или подсказки – используйте свои собственные способности! Наш мозг и так очень мало напрягается в современном мире, так почему бы не использовать редкую возможность размять его при помощи этой великолепной логической задачи?!

Если вам понравилась эта задача на логику – поделитесь ею с друзьями в социальных сетях. Если вам вообще нравятся логические задачи и головоломки, – подписывайтесь на сайт interesnyefakty.org. С нами всегда интересно!

Понравился пост? Нажми любую кнопку:



Интересные факты:

Похожие факты:

А что вы думаете об этом?
  • http://vk.com/id194323595 Станислав Ковалев

    Поставить на весы один мешок взвесить, далее снять тару и поочередно ставить оставшиеся.

    • Модератор

      Прочитайте внимательно главное условие.

      • Станислав

        Но это не нарушило главного условия

        • Модератор

          Это нарушило именно главное условие (о единократном взвешивании).

          • А

            5

  • Ширяев Александр

    Из каждого мешка возьму то количество монет, которое соответствует номеру мешка, и помещу их в 10 мешок соответственно, взвешу и получу сумму из трёх чисел, последняя единица будет соответствовать номеру мешка, в случае если это будет 0, это десятый мешок! Думаю понятно.???

    • http://vk.com/id552380964 Михаил Бо

      Я так же решил, только порядок мешков в обратную сторону с первого по девятый. Поэтому объяснение более громозским вышло)

    • http://vk.com/id599059446 Михаил Коваленко

      при условии что количество монет равняется номеру мешка всё будет верно, но его тут нет. 550 + ( 2*10 + 2*11), то получается 2 мешок хотя должен быть 4. Критика приветствуется

    • Аноним

      Krasavcek!

  • Игорь Коваленко

    С каждого мешка брать по одной монете и ложить на весы. Когда попадет фальшивая, оно покажет?

  • Ирина

    Я бы поставила все 10 мешков на весы одновременно (это же считается за одно взвешивание?) и убирала бы по одному мешку, как только весы показали что я убрала с весов мешок весом 110 граммов, а не 100, значит это и есть фальшивый мешок

  • Morgan

    Взять с каждого мешочка по 1 монете, положить их в ряд на весы, в соответствии с поочерёдностью мешочков, и отнимать с весов по 1 монете, и как только будет видно что при снятии монеты на весах убавилось 11 грамм вместо 10, смотрим какая это монета по счёту была, такой и мешок.

    • Модератор

      Перечитайте условия

      • Morgan

        Часть условия про весы не понятна. Что значит «взвешивание можно произвести 1 раз»? 1 раз положить что то на весы? или один раз снять с весов результат взвешивания? и весы какие? гуси, или електронные?

      • http://vk.com/id490107923 Пётр Лапко

        кстати ,а как быть с «правильным» решением.Ведь монета фальшивка останется среди настоящих.

  • Скользкий

    свалить все монеты в 1 мешок, в этом мешке фальшивки и будут.

    • Nadine

      Точно. Я тоже хотела это предложить

  • Виктория

    Мне кажется нужно из каждого мешка достать кол-во монет, соответствующее номеру на мешке. И все взвесить. Итого мы взвесим 55 монет. Если бы вес каждой монеты был бы 10 гр., то общий вес 550. Но т. к. Среди них есть фальшивые( предположим, из 5-го мешка) тогда общий вес будет 50 шт * 10 гр + 5 шт * 11 = 555. Если вес будет, например, 557, то 7 мешок выходит ну и т.д…

    • Сергій

      Згоден, тільки треба з 9 мішків брати, з десятого немає сенсу.

  • http://vk.com/id552380964 Михаил Бо

    Надо из первого мешка переложить 9 монет. По одной в каждый из остальных 9-ти мешков. Из второго мешка переложить 8 монет, включающих в себя переложенную из первого. По одной в каждый следующий мешок. Из третьего — 7 монет, включая переложенные из предыдущих мешков, по одной в каждый следующий мешок. И так до девятого мешка, пока в десятом не окажется 19 монет, а в каждом предыдущем на две монеты меньше чем в следующем. После этого надо взвесить один раз десятый мешок. Если он весит 199 грамм, то фальшивые монеты были в первом мешке. Если 198 грамм, то во втором и так далее до девятого мешка. Если же десятый мешок весит 200 грамм, то фальшивые монеты были в нем.

  • https://www.facebook.com/app_scoped_user_id/839406262773063/ Oleg Mechetin

    Не указано главное условие весы электронные а не сравнение одних мешков с другими . Задача имеет решение только с эталоном извне .

  • Theofanis Papadopoulos

    Взять из первого мешка одну монету, из второго две…из девятого 9 момент. Десятый мешок оставить как есть. Взвесить 45 монет. Если они будут весить 450 граммов, то фальшивые в 10 мешке. Если будут весить 451 граммов, то фальшивые в первом, если 452 тогда фальшивые во втором….если будут весить 459 тогда фальшивые в девятом.

  • Аноним

    я предположу,что можно пойти следующим путем
    зная что в 9 мешках из 10 (настоящие монеты-не важно в каких) ,то 10 монет умножаем на 10 грамм = 900 грамм
    10 мешке монеты по 11 грамм,т.е 10 умножаем на 11=110
    900 грамм +110 =1010 грамм
    далее помещаем все мешки на весы и видим на них 1010 грамм.
    по условию задачи мы должны произвести одно взвешивание,мы его сделали.
    теперь из условий задачи следует,что можно сколько угодно вынимать,перекладывать и помещать обратно монеты,а это значит ,что вынимания монетку из определенного мешка под номером нам будет понятно в каком мешке фальшивые монетки, так как в 9 из 10 случаев будет значение 1000 грамм, а в одном из 10 будет значение 999.
    я считаю,формально .измерить это поместить что-либо на весы.далее не снимая мешков с весов ,производить перекладывание монет.

  • Аноним

    Раз по условию задачи в десяти изображенных мешках по 10 монет по 10 грамм, то мешок с 10 фальшивыми монетами по 11 грамм является одиннадцатым, который не указан на картинке. Отсюда вывод — у задачи нет решения выявить мешок с фальшивыми монетами. Либо ответ — все мешки с картинки с настоящими монетами.

  • http://vk.com/id2450059 Александр Гуров

    Ставить на весы поочередно все мешки. То есть мы не снимаем мешки, а просто добавляем мешки. Таким образом взвешивание всего одного. И когда появится мешочек с лишней массой, мы сразу узнаем, что там — фальшивка.

    • Дедужко Ху

      Тоже так было подумал. И всё ж это серия взвешиваний. Одно взвешивание подразумевает один результат.

  • Азат Альбертович

    Взвешываем 5 мешков, если вес составляет 500 гр. значит фальшивые в незвешыных мешках если 510 то в этих 5 мешках. Мешки с нормальными манетами убираем в сторону. Берем из 5 оставшихся 2 мешка, взвешиваем. Если фальшивка там то вес будет 210 грамм если же нет то 200 . Соответственно если фальшивые среди этих 2 мешков то не составить трудности найти среди них где какой, так как осталось одно взвешивание если же нет, то, из оставщихся трех допустим они под номерами 1,2,3 ( для упрощения) из 1 по одной монете кладем во 2 и 3 . И взвешиваем 3 мешок, если в 1 фальшивые то вес будет 111гр. если нет то 110 и фальшивые в 2 . Если же фальшь в 3 мешке то вес будет 120 грамм.

  • Олег Белоус

    Задача противоречива, а потому нерешаема. Первое утверждение, что есть 10 пронумерованных мешков, в каждом из которых находится по 10 золотых монет, каждая из которых весит 10 граммов противоречит второму, где говорится что в каком-то мешке монеты весят уже по 11 граммов.
    Если бы задача была составлена так: Перед нами 10 пронумерованных мешков, в ДЕВЯТИ (а не каждом) из которых находится по 10 золотых монет. Каждая монета весит 10 граммов. В одном из мешков находятся фальшивые монеты. По виду они ничем не отличаются от настоящих, вот только весят они не по 10, а по 11 граммов, тогда можно было бы думать над решением.

  • http://vk.com/id599059446 Михаил Коваленко

    раз можно перекладывать из мешка в другой, то в номер 1 складываем всё( не сказано про размер мешка, так что представляем его бездонным или достаточным для 100 монет) ответом будет первый мешок

    • Дедужко Ху

      И можно не взвешивать)))) По-моему, имелось ввиду, в каком мешке фальшивки лежат изначально? Не?

  • Аноним

    Доброго времени суток, интеллектуалы! Я мастер в этом деле и поэтому слушайте моё грандиозное решение: В первом мешке оставляем 1 монету, а девять добавляем с 9го. Во втором мешке оставляем 2 монеты, а остальные восемь добавляем с 8го мешка. Потом 3+7; 4+6; в пятом просто убираем 5 монет, а десятый вообще не трогаем. Теперь ставим на весы 1,2,3,4,5 и 10 мешки. И, уаля, — количество лишних граммов выдаст номер мешка с фальшивыми монетами!

  • Аноним

    Пусть весы показывают вес, а не больше-меньше, тогда взвешивание нужно одно.
    Берём на ЕДИНСТВЕННОЕ взвешивание из каждого мешка монеты согласно номеру мешка: из 1го мешка 1 монету, из 2го — 2, из 3го — 3 и т.д. Из последнего мешка 0 монет.
    Всё монеты, не перемешивая (чтобы можно было потом вернуть фальшивые назад), кладём на весы.
    Вес всех монет, кроме фальшивых, кратен 10. Каждая фальшивая монета +1 гр, а значит «лишние» граммы (сверх десятка) указывают на номер мешка с фальшивыми монетами. Если результат взвешивания кратен 10, то Фальшивые монеты в 10м мешке.

    • Аноним

      А если не кратен 10,как по собранным из мешочков монетах определить среди них монеты из фальшивого мешочка?

  • Аноним

    Кладём 5 мешочков на одну сторону весов. 5 мешочков на другую. Естественно, одна из кучек мешков перевесит, так как в ней будет находиться тот самый «тяжёленький» мешочек (с фальшивками)… Взвешивание состоялось.
    Теперь убираем по одному мешку с каждой стороны весов достигая равновесия. Как только оное состоялось, значит с соответствующей кучки был снят искомый дисбалансный (110-грамовый)мешок .

    • Vladi Vas

      Здравствуйте! Опишите, пожалуйста, свой ход мыслей, как пришли к такому решению? Может жизненный опыт какой сподвиг..

    • Аноним

      Мешочки убирать нельзя, только перекладывать монеты

    • Дедужко Ху

      А у меня весы с одной чашей, на которую давишь. и стрелка показывает вес. Не сильно помогло твоё замудрюченное решение.

  • Аноним

    Допустим, весы показывают вес.
    Положим в первый и шестой мешок 1 монету, во второй и седьмой — 2 монеты…в пятый и десятый — 5 монет . Размещаем на чашах весов по половине мешков. Разряд единиц значения перевесившей группы будет соответствовать номеру мешка с фальшивыми монетами(если перевесили мешки с шестого по десятый, то к единицам надо прибавить 5, результат 0 указывает на 10-й мешок)

  • Аноним

    По условиям задачи, в каждом мешке 10 золотых монет плюс в одном из них фальшивые монеты, поэтому в том мешке где больше 10 монет и находится фальшивка.

  • Аноним

    Убираем из 1-го мешка 1 монету, из 2-го мешка 2, из 3-го 3 и так далее. Из 10-ого мешка не убираем монеты. Взвешиваем все мешки вместе. По весу определяем в каком мешке фальшивые монеты. Если вес оканчивается на 9 то в первом , если на 8, то во втором и так далее.

    • Аноним

      чушь полная. По какому весу определяем?

  • Аноним

    Поставить все мешки на весы и поочередно вынимать из каждого по одной монетке. По сути взвешивание одно

    • Аноним

      это серия взвешиваний

  • Аноним

    Из мешка №10 высыпаем все монеты. Кладем в мешок №10 одну монету из мешка №1, две монеты из мешка №2, три монеты из мешка №3 … девять монет из мешка №9. Взвешиваем мешок №10. Смотрим на крайнюю правую цифру на весах. Если она равна 3, то фальшивые монеты были в мешке №3. Если 8, то в мешке №8. Если она равна 0, то фальшивым был мешок №10, из которого мы высыпали все монеты. Не слишком сложная задача, но интересная.

  • Аноним

    Здорово ребятки..Будем учиться думать логически

Top